Andrew Kingdom
Some mathematical finds I’ve made over the years.
By Andrew Kingdom. (I’ll update the details when I have time.)
Four-colour theorum formula
The four-colour theory states that any map can be coloured in using a maximum of four colours without using the same colour for neighbouring regions. This has been proven using a computer.
My discovery was a partial-geometric method (collapsing all combinations down to a single set of incomplete-shapes) to prove all combinations on paper, which I believe hadn’t been done previously. This can also be done using a divided 2D toroidal (donut) shape series, but I’m not 100% sure it covers all possibilies.
Circa 2007
Hexagonal Conway’s Life
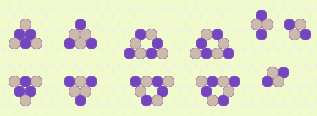
Cellular automaton based on a six-sided grid rather than John Conway’s orthogonal grid. It occurred to me that Conway’s rules were imbalanced and that a hexagonal structure was more natural and stable, which proved to be the case and the rules are much simpler.
(Published online in 2003.)
Primality test formula
My discovery was essentially the same as Wilson’s theorum, (p−1)!≡−1(mod p).
(Published in maths groups online circa 2000.)
Pythagorean Triple Integers
These are numbers that perfectly fulfil the ‘Pythagorus’ formula a2 + b2 = c2.
Example: (3,4,5) meaning 3 x 3 + 4 x 4 = 5 x 5.
These were discovered by the ancient Egyptians, Babylonians and others.
My discovery was a simple set of formulas to generate all possible integer triples, loosely similar to the following: a=k(m2−n2), b=2⋅k⋅m⋅n, c=k(m2+n2), where k is a multiplier.
(Published in maths groups online circa 1988.)